I’ve always been fascinated by variations on the fundamental tools of the game. Earlier this week I looked at a more recent mechanic in-depth, but early on, I really didn’t have a firm grasp of what made a mechanic interesting or useful. The sweet spot seems to be around 3d6 mod 10, where the curve is more-or-less inverted and symmetrical. But the smaller the modulus, the flatter the curve, so this may have limited application.

Recovered: Modular Dice

I’ve been using “d50”s without noticing for some time. You can get huge, strange 50-sided dice I’m sure, but that’s not what I’m talking about. Instead, I roll d% and if the tens-place is greater than 5, I “wrap around.” I’m sure this is something that’s not uncommon, and it saves re-rolling if the die is an even multiple.

I decided to investigate this further. For a uniform distribution it’s not that interesting, but starting from a normal distribution it’s a neat way to get two peaks. Figure 1 shows the effects of different moduli on the 3d6 distribution.

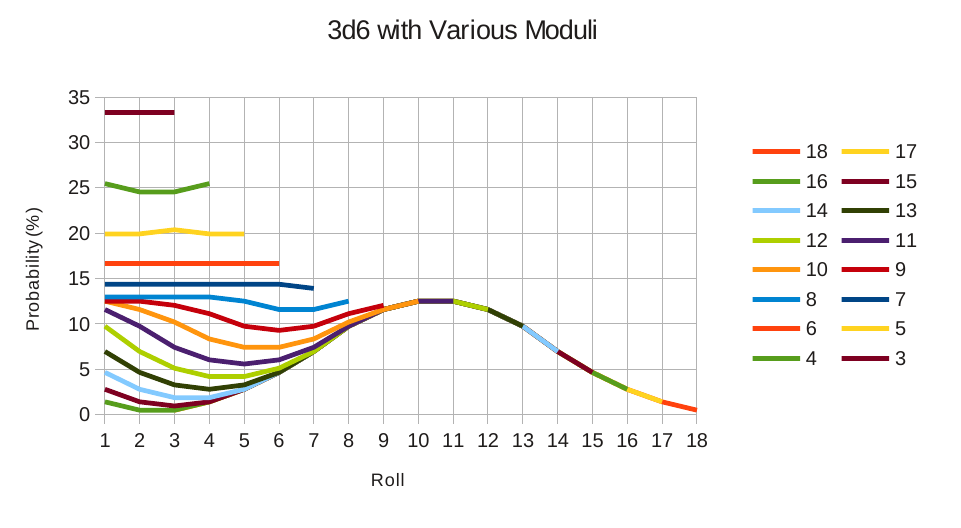Figure 1.

If you’d like to play with this in AnyDice, here’s the function I’ve written:

function: A:n mod B:n {
    if A > B {result: [(A - B) mod B]}
    result: A
}

This post was first shared on August 21, 2012.

---

---

---

---

---

---