New Year’s Resolution Mechanic: Clashing
W.F. Smith of Prismatic Wasteland challenges everyone to describe a novel resolution mechanic, name it, and blog it.
Fight between Goku and Frieza by SotoDraw, CC BY-NC-ND-3.0, via DeviantArt.
I want a fighting mechanic that can capture the power scaling of a shōnen manga without being miserable to play. It’s gotta have a dumb multiplier, but it needs some plausible nod towards “bounded accuracy.”
This mechanic is an opposed roll.
Each participant rolls a number of dice, sums the result, and multiplies it by a constant multiplier. The higher number wins, with some element needed to break ties. The number of dice starts at 1, and goes up to 5 based on various story factors. The multiplier starts at 1 and goes up to 5 based on various mechanical factors.
Let’s look at how three different players match up. Player A only takes story advantages (varying number of dice in their pool). Player B only takes mechanical advantages (varying their multiplier). And Player C never takes any advantages (rolling only 1d6).
In the matchup between Player A (story) and Player C (unmodified), Player A quickly outmatches Player C. The odds that Player C wins against a full pool (5d6) are infinitesimal (). Including a tie, the odds are still only ~0.02%.
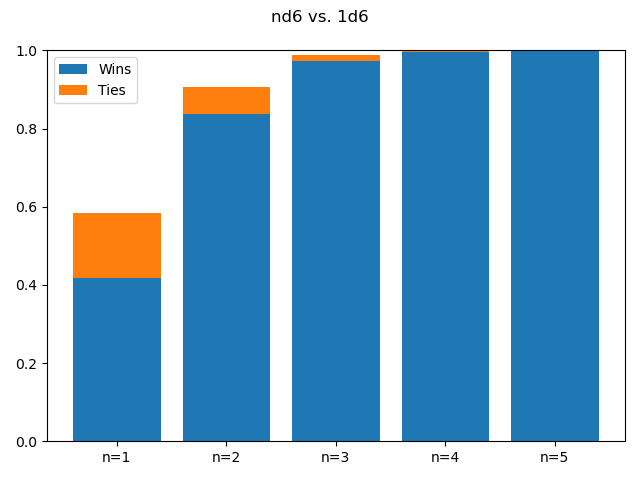
In the matchup between Player B (mechanics) and Player C (unmodified), Player C remains possibly relevant to the very end. Player C beats a roll with maximum multiplier (1d6*5) about 5% of the time, the odds of a “natural 20.”
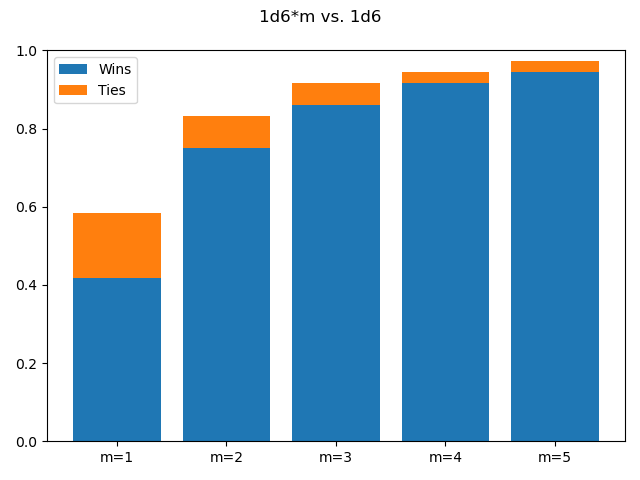
Ignoring ties, it’s even possible to roughly visualize the matchup between Players A and B.
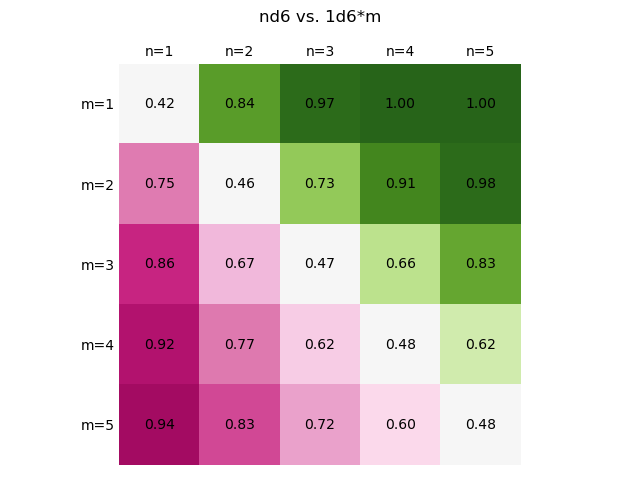
Here, green squares are victories for Player A, pink squares are victories for Player B, and the white diagonal squares are ties. The numbers shown are the odds of that victory (or the odds of either victory in the case of a tie).
As always, the code is in a gist. I used dyce, which was pretty good for this.