Recovered: Black Ships and Bad Hydrodynamics

I was going to make a quick fun game about boats. Treasure Island, The Odyssey, One Piece. I wasn’t going to get caught up in the details of how boats work. I told myself this at the outset, and believed it. I was going to borrow liberally from other, nicer rulesets, and not worry about realism. Now I’m writing about boat hydrodynamics.

When Viking explorers found new lands, they were usually about a week’s sailing away. More distant lands were reached by following a chain of smaller stops. This is because they could survive for about two weeks at sea, so one week was the point of no return.¹ Rather than start with existing historic boats, we can take this type of exploration as our goal, and then work out how best achieve it.

The Draken Harald Hårfagre

Some Rules

I haven’t playtested these, they’re just draft rules.

• Every week, the crew² rolls against mishaps. An undercrewed ship rolls with disadvantage.
• An overburdened ship moves at half speed.
• When there are fewer sacks³ of supplies than people, the ship is at half rations. At half rations, all ability checks are rolled at disadvantage. For each additional week at half rations, an additional die is added to the disadvantage (e.g. on two weeks of half rations, an ability check is the worst result of three dice). This assumes some kind of subsistence fishing, scavenging, rationing, etc. This doesn’t kill you directly, but you’re going to die.

Mishaps

1. 1d4 sacks of supplies lost or spoiled
2. ship damaged - move at half speed (rigging, rudder, etc.)
3. you are lost
4. injury among the crew
5. disease among the crew
6. stowaway found
7. becalmed for 1d6 days
8. ill omen - next mishap check at disadvantage unless the crew makes appropriate supplication

Encounters

Encounters at sea are never by surprise excepting with beasts, and evasion is down to chance (1d4 to evade: on a 1, success, on a 2, success but off-course or lost day).

1. Global Faction
2. Local Faction
3. Foreign Faction
4. Unaffiliated
5. Wild
6. Flotsam or sign

Exploration Sailing

Going back to “islands are a week away,” we can interpret this two ways, which I will call the “dense ocean” assumption and the “sparse ocean” assumption. Given the distances and speeds involved, the classical 6-mile hex quickly becomes more hindrance than help, and instead everything is worked out in points and lines. Obviously all these assumptions are different for large ships with large crews, but I don’t think those are conducive to the game I’m trying to make here. It’s also worth noting that I’m explicitly fitting the geography to the type of game I want to run here, not to any kind of reality.

Visibility

A person can see d km away on a clear day at sea, where

${\displaystyle d=\sqrt{13h}}$

and

• $d$ is distance seen (km) and
• $h$ is the height above sea level (m).

This means:

• A 2-meter person standing at roughly sea level can see 5 km.
• A person standing atop a 30 m crow’s nest can see 20 km.
• In ideal conditions, smoke rises to a mixing height of 518 m, so can be seen from 82 km away.
• A bird flying at 4000 m can see and be seen from 228 km away.

The Dense Ocean

On average, there is an island one week’s travel in any direction.

This means that each day of exploration, there is a 1-in-7 chance of finding an island. Call it 1-in-8 (to fit the dice) and be done with it.

The Sparse Ocean

On average, the nearest island is 1 week away.

This means that in a circle of radius one week’s travel, there will be an expected two islands (start and destination). Here I will make a series of poor assumptions which allow me to simplify my calculations: Assume that the ship will sail in a straight line each day in one of eight directions, and that it will see everything there is to see in that direction. The area seen in one day is then

${\displaystyle A_{day}=\frac{1}{8}\pi {\left(\frac{1}{7}r\right)}^2}$

where

• $A_{day}$ is the area of ocean seen in one day, and
• $r$ is the distance traveled in one week.

Then the probability of finding an island in a week is

${\displaystyle P_{week}=2\frac{7\left(\frac{1}{8}\pi {\left(\frac{1}{7}r\right)}^2\right)}{\pi r^2}=\frac{1}{28}}$

and the probability of finding an island on any given day is

${\displaystyle P_{day}=\frac{1}{7}\times \frac{1}{28}=\frac{1}{196}}$

Exploration sailing is terrible using a sparse ocean.

What about Vikings?

The Draken Harald Hårfagre has a top speed of 14 knots or 25.928 km/hr. If the crew never rests, then the ship could travel 4356 km in a week. If they use birds to find land, then they explore a swath of ocean 4356 km x 2(228) km in one week. The probability of finding an island is then

${\displaystyle P_{week}=2\frac{2dr}{\pi r^2}=2\frac{2(228)(4356)}{\pi (4356{)}^2}=\frac{912}{4356\pi }\approx 0.0666}$

and

${\displaystyle P_{day}=\frac{1}{7}{P}_{week}\approx 0.01}$

This is about twice as good odds as with worse assumptions, but still doesn’t seem great. I’m sure that realistic exploration sailing had any number of other factors going for it and the math here is all wrong, but for my purposes the Dense Ocean seems more fun anyway.

How Much?

Assume a party of 5 people. We’ll say that a week’s supplies for one person is a sack, and in addition each person has a sack of tools and gear. So our small ship must now carry 20 sacks of weight (5 people, 10 supplies, 5 gear).

Old ships are measured in tonnage,⁴ the number of tun-casks the ship could fit. From this random image I found, a tun cask takes four people to carry, so is equivalent to 4 sacks. Therefore our small ship is 5 tons.

I no longer know the source of this image, but it's too important to readily cut.

How Fast?

An early limitation on ship speed is the “hull speed,” where

${\displaystyle V_{hull}=1.34\sqrt{L_{WL}}}$

and

• $V_{hull}$ is the hull speed (knots), and
• $L_{WL}$ is the length of the ship measured at the waterline (ft).

Strictly speaking this isn’t a “limitation,” but I must stress that we’re talking about terrible boats here.

From the tonnage, we can back-calculate the length of the ship using the Builder’s Old Measurement

${\displaystyle T=\frac{(L_{OA}-\frac{3}{5}b)b\frac{b}{2}}{94}}$

where:

• $T$ is the tonnage (tons burden),
• $L_{OA}$ is the over-all length of the ship (from stem to stern-post, ft), and
• $b$ is the beam, or width of the ship (ft)

and also a random rule-of-thumb found on Wikipedia somewhere

${\displaystyle b=\sqrt[3]{L_{OA}^2}+1}$

($L_{OA}$ and $b$ in ft). Finally, we must assume that, for our purposes, the waterline length is equal to the overall length ($L_{WL}=L_{OA}$). This isn’t a great assumption, but it’s not terrible if our boat is built more like a bathtub than a canoe.

With all of this, I wrote a quick octave script to generate the following table

$T$ (tons)	$L_{OA}$ (ft)	$V_{hull}$ (knots)
1	9.5255	4.1357
2	12.837	4.8011
3	15.294	5.2404
4	17.319	5.5766
5	19.074	5.8523
6	20.639	6.0876
7	22.061	6.2939
8	23.372	6.4782
9	24.593	6.6453
10	25.739	6.7983

At this point, I started to think I might have lost track of where I started, so I stopped. When someone asked “how fast do boats go” on a Discord server, I just pointed them at this table from Labyrinth Lord:

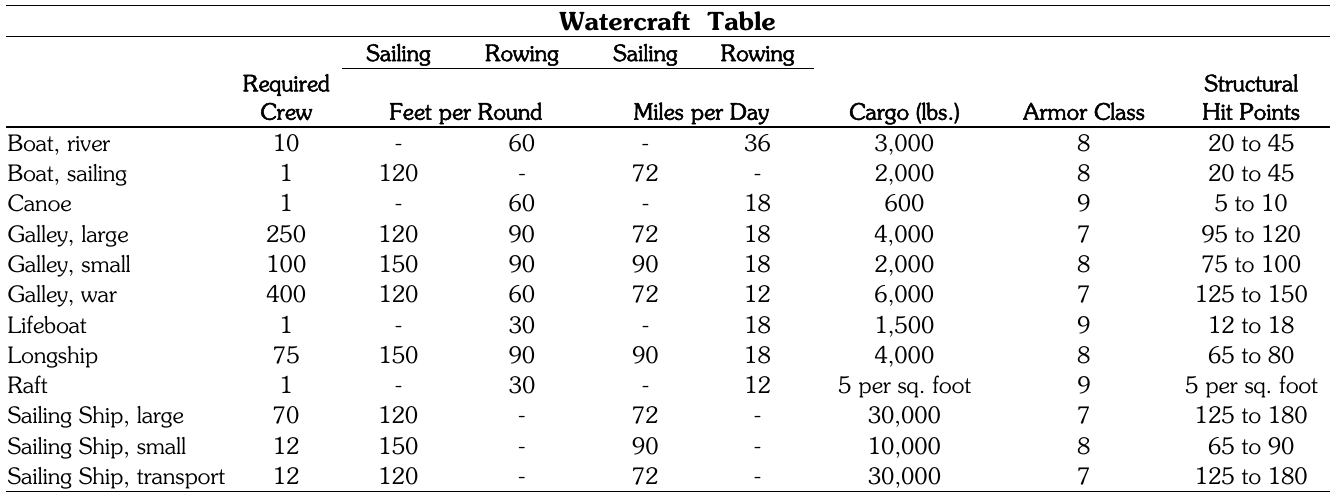Labyrinth Lord's Watercraft Table

This post was first shared on August 18, 2019.

---

1. This is what the tour guides of The Draken Harald Hårfagre told me, but I might be misremembering.↩︎

2. Following from Ultraviolet Grasslands (UVG), a “group” check rotates throughout the crew.↩︎

3. Sacks are another useful abstraction from UVG. A sack is: as much as one person can carry unencumbered; all of a person’s professional gear; one unconscious human; one unit of trade goods; or enough food, water, and consumables for one person to survive for one week.↩︎

4. These are tons burden (a volume measurement), as opposed to tons displacement (a weight measurement). As an engineer, it distresses me the number of meanings that “ton” can take, but here it is unavoidable.↩︎

---

---

---

---

---