Recovered: 7d6, split between two attributes
On 20 Feb 2020, PlanetNiles (Ey/Em) NB on the workshop channel of the OSR Discord asked:1
7d6, split between two attributes
What values are even possible?
One way to think about this is not in terms of the values themselves, but in terms of the difference between the two paired attributes. The maximum difference is when all dice are allocated to one attribute, leaving the other empty. This is then equivalent to the sum of the dice.
The minimum difference between the two is a form of the well-studied partition problem: given a set of numbers, can it be split into two sub-sets with equal sums? A heuristic method that can usually2 find the smallest difference between our two subsets (and therefore if they can be equal or not) is called the Karmarkar-Karp method, which works as follows:
- Take the two largest numbers in the set. Assume that these will go in opposite partitions.
- Because they will go in opposite partitions, we subtract them from each other.
- Instead of now deciding which partitions they will go in, we return the difference between them to the set. This is effectively deferring that decision until later.
- Repeat steps 1-3 until there are only two numbers left. The difference of these last two numbers is the smallest difference we can make with this set.
Note that we didn’t actually find what the partitions are, only what the difference between them is here. I hope this is clear enough, but I’m also sure that clearer explanations can be found with minimal searching.
With some wrangling, we can produce this lovely chart, where a heavier hexagon is a more likely pairing.
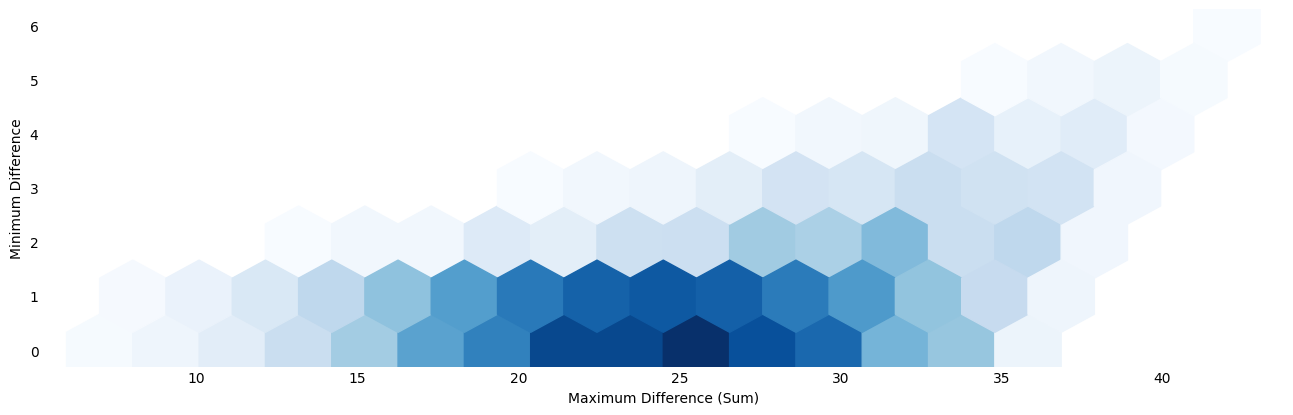 Figure 1. Hexagons are elegant, as odd/even combinations that cannot occur are skipped naturally.
Figure 1. Hexagons are elegant, as odd/even combinations that cannot occur are skipped naturally.
From this, it looks like the system gives a lot of flexibility in assigning scores to your attributes.
What Values are Likely?
I have a concern about this mechanic though: if you give someone a range of numbers, and tell them to pick one, they will tend to pick in the middle.3 If a player is dead-set on being boring, how boring can they be?
It might not be exactly true, but we can show the distribution of all the high stats and all the low stats together, and then compare them to the distribution of 7d6 literally divided in half (which is approximately normal).
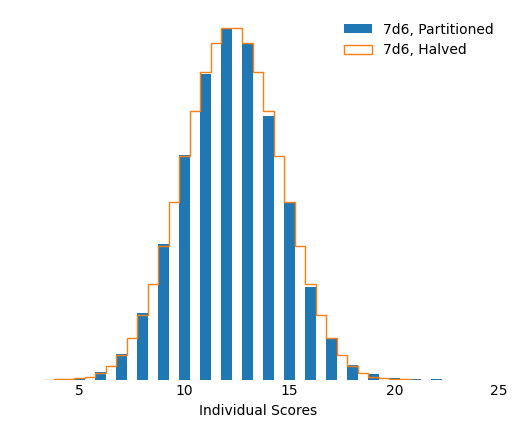 Figure 2.
Figure 2.
This doesn’t look great, but PlanetNiles has actually already got us covered here:
Of course. I’d further consider including subsystems where the difference between attributes had some sort of effect. So favoring one over the other would prove beneficial in some way, or at least open up different options.
The strength of this mechanic then will rely on the strength of the system. Given the range of the first figure though, I have confidence that an interesting system could be built here.
What about other mechanics?
Suppose we were looking for a similar mechanic, except that it would force a difference between the attributes where possible. We might expect intuitively, that fewer dice and larger dice are harder to partition effectively. This table gives the probability of a forced difference (although does not consider the size of that difference).
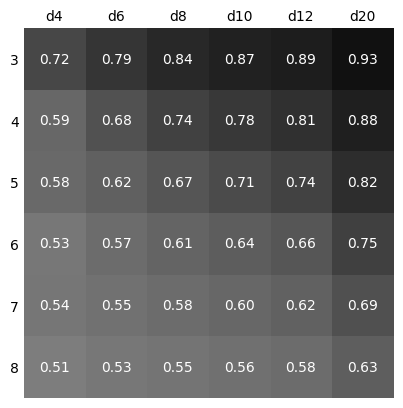 Figure 3.
Figure 3.
From this table, I thought I would look at 3d20, because it forces a difference the most often. The figures below have the same interpretations as the similar ones above, but for 3d20 instead of 7d6.
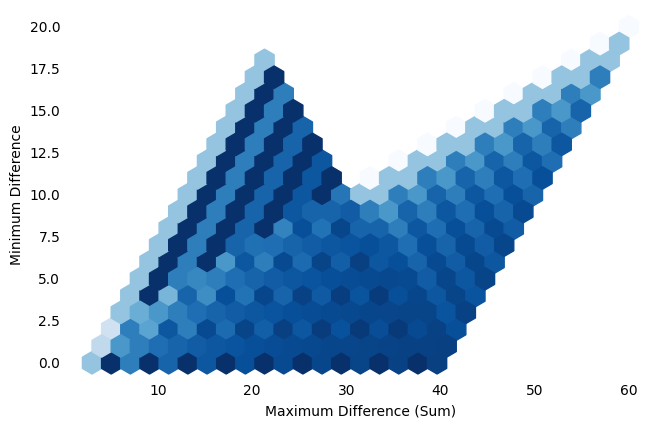 Figure 4.
Figure 4. 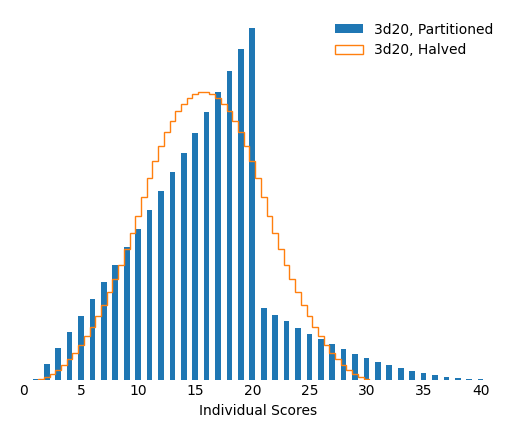 Figure 5.
Figure 5.
Python
This was my first project using Python, and I think it’s an all right language. It’ll probably displace Octave in my repertoire, but I’m sure I’ll be right back at Perl if I start doing string stuff again. The code’s a bit janky, but you can take a look here.
This post was first shared on March 24, 2020.
“Asked” a little more directly this time, if only because I asked first.↩︎
According to Wikipedia, this method is “bad for instances where the numbers are exponential in the size of the set,” so like, probably fine?↩︎
I only know this anecdotally: if you tell a plant operator to keep some process temperature between a high limit and a low limit, without fail they will control it to the middle of the two. It makes sense to a person, but the optimal temperature is provably at one of the two extremes. Possibly, this is an extension of the anchoring effect.↩︎