Recovered: 5d6 but only count straights and matching

On 7 Feb 2020, diregrizzlybear on the GLOG channel of the OSR Discord asked:¹

5d6 but only count straights and matching.

One solution might be to list all the rolls and score each one. This is probably feasible with a script. Instead, I enumerated the “hands,” and then found the probabilities of each of those.

Hands with No Degrees of Freedom

Run of Five

There are only two runs of five: ⚀⚁⚂⚃⚄ and ⚁⚂⚃⚄⚅. There is only one way to “make” each of these hands (“Count”), but because each die has a different face, there are 5!=120 possible orderings of each hand (Permutations).

Hand	Score	Count	Permutations	Odds
⚀⚁⚂⚃⚄	15	1	120	120
⚁⚂⚃⚄⚅	20	1	120	120

Quintuple

There are six possible quintuples, and again, there is only one way to construct each one. While there are 5! possible orderings of five dice, because five of them are interchangeable, there is only one possible ordering of a quintuple (5!/5!=1), which makes a quintuple much less likely than a run of five.

If this seems counter-intuitive, consider rolling one die five times in order. If your first roll is a ⚀, to eventually score quintuples, the next roll must also be a ⚀ (1/6 odds). To eventually score a run of five, the next roll must only be not ⚅ or ⚀ (4/6 odds).

Hand	Score	Count	Permutations	Odds
⚀⚀⚀⚀⚀	5	1	1	1
⚁⚁⚁⚁⚁	10	1	1	1
⚂⚂⚂⚂⚂	15	1	1	1
⚃⚃⚃⚃⚃	20	1	1	1
⚄⚄⚄⚄⚄	25	1	1	1
⚅⚅⚅⚅⚅	30	1	1	1

Run of Three + Double

There are 24 ways to score a run of three + double: 4 runs of three and 6 doubles. Depending on the doubled number, it may be possible to score this as other hands (run of four, triple), but this is never advantageous.

Because of the doubled number, there will be fewer ways to order this hand than a run of five, but more than a quintuple. If the doubled number is in the run, there are 5!/3!=20 possible orderings, and if it is not, then there are 5!2!=60.

Hand	Score	Count	Permutations	Odds
⚀⚁⚂⚀⚀	8	1	20	20
⚀⚁⚂⚁⚁	10	1	20	20
⚀⚁⚂⚂⚂	12	1	20	20
⚀⚁⚂⚃⚃	14	1	60	60
⚀⚁⚂⚄⚄	16	1	60	60
⚀⚁⚂⚅⚅	18	1	60	60
⚁⚂⚃⚀⚀	11	1	60	60
⚁⚂⚃⚁⚁	13	1	20	20
⚁⚂⚃⚂⚂	15	1	20	20
⚁⚂⚃⚃⚃	17	1	20	20
⚁⚂⚃⚄⚄	19	1	60	60
⚁⚂⚃⚅⚅	21	1	60	60
⚂⚃⚄⚀⚀	14	1	60	60
⚂⚃⚄⚁⚁	16	1	60	60
⚂⚃⚄⚂⚂	18	1	20	20
⚂⚃⚄⚃⚃	20	1	20	20
⚂⚃⚄⚄⚄	22	1	20	20
⚂⚃⚄⚅⚅	24	1	60	60
⚃⚄⚅⚀⚀	17	1	60	60
⚃⚄⚅⚁⚁	19	1	60	60
⚃⚄⚅⚂⚂	21	1	60	60
⚃⚄⚅⚃⚃	23	1	20	20
⚃⚄⚅⚄⚄	25	1	20	20
⚃⚄⚅⚅⚅	27	1	20	20

Triple + Double

There are 30 ways to score a triple + double: 6 ways to score one and then 5 remaining ways to score the other (to exclude quintuples, which are already accounted for). As with run of three + double, we must account for duplicated numbers when counting orderings. There are then 5!/(3!*2!)=10 permutations of each.

Hand	Score	Count	Permutations	Odds
⚀⚀⚀⚁⚁	7	1	10	10
⚀⚀⚀⚂⚂	9	1	10	10
⚀⚀⚀⚃⚃	11	1	10	10
⚀⚀⚀⚄⚄	13	1	10	10
⚀⚀⚀⚅⚅	15	1	10	10
⚁⚁⚁⚀⚀	8	1	10	10
⚁⚁⚁⚂⚂	12	1	10	10
⚁⚁⚁⚃⚃	14	1	10	10
⚁⚁⚁⚄⚄	16	1	10	10
⚁⚁⚁⚅⚅	18	1	10	10
⚂⚂⚂⚀⚀	11	1	10	10
⚂⚂⚂⚁⚁	13	1	10	10
⚂⚂⚂⚃⚃	17	1	10	10
⚂⚂⚂⚄⚄	19	1	10	10
⚂⚂⚂⚅⚅	21	1	10	10
⚃⚃⚃⚀⚀	14	1	10	10
⚃⚃⚃⚁⚁	16	1	10	10
⚃⚃⚃⚂⚂	18	1	10	10
⚃⚃⚃⚄⚄	22	1	10	10
⚃⚃⚃⚅⚅	24	1	10	10
⚄⚄⚄⚀⚀	17	1	10	10
⚄⚄⚄⚁⚁	19	1	10	10
⚄⚄⚄⚂⚂	21	1	10	10
⚄⚄⚄⚃⚃	23	1	10	10
⚄⚄⚄⚅⚅	27	1	10	10
⚅⚅⚅⚀⚀	20	1	10	10
⚅⚅⚅⚁⚁	22	1	10	10
⚅⚅⚅⚂⚂	24	1	10	10
⚅⚅⚅⚃⚃	26	1	10	10
⚅⚅⚅⚄⚄	28	1	10	10

Hands with One Degree of Freedom

Run of Four

There are three possible runs of four: ⚀⚁⚂⚃x, ⚁⚂⚃⚄x, ⚂⚃⚄⚅x, where x is our “unfixed” die (our degree of freedom). If x is equal to either the highest or lowest element of the run, then we instead have a run of three + double. If it is equal to a number after either end of the run, then we instead have a run of five. So for ⚀⚁⚂⚃x and ⚂⚃⚄⚅x, x has three possible values, and for ⚁⚂⚃⚄x, x has two possible values. We will also consider the cases where x is “inside” the run and “outside” the run separately, as the number of permutations is different.

Hand	Score	Count	Permutations	Odds
⚀⚁⚂⚃x;x∈{⚁,⚂}	10	2	60	120
⚀⚁⚂⚃x;x=⚅	10	1	120	120
⚁⚂⚃⚄x;x∈{⚂,⚃}	14	2	60	120
⚂⚃⚄⚅x;x∈{⚃,⚄}	18	2	60	120
⚂⚃⚄⚅x;x=1	18	1	120	120

Quadruple

There are 6 possible quadruples, with 5 ways to construct each one (again, to exclude quintuples). There are 5!/4!=5 permutations of a quadruple.

Hand	Score	Count	Permutations	Odds
⚀⚀⚀⚀x	4	5	5	25
⚁⚁⚁⚁x	8	5	5	25
⚂⚂⚂⚂x	12	5	5	25
⚃⚃⚃⚃x	16	5	5	25
⚄⚄⚄⚄x	20	5	5	25
⚅⚅⚅⚅x	24	5	5	25

Two Doubles

There are 15 ways to score two doubles (half as many as triple + double, because it doesn’t matter which number is the first multiple and which number is the second). The unfixed die (x) can take any of the four remaining values.² A hand of two doubles has 120!/(2!*2!)=30 permutations.

Hand	Score	Count	Permutations	Odds
⚀⚀⚁⚁x	6	4	30	120
⚀⚀⚂⚂x	8	4	30	120
⚀⚀⚃⚃x	10	4	30	120
⚀⚀⚄⚄x	12	4	30	120
⚀⚀⚅⚅x	14	4	30	120
⚁⚁⚂⚂x	10	4	30	120
⚁⚁⚃⚃x	12	4	30	120
⚁⚁⚄⚄x	14	4	30	120
⚁⚁⚅⚅x	16	4	30	120
⚂⚂⚃⚃x	14	4	30	120
⚂⚂⚄⚄x	16	4	30	120
⚂⚂⚅⚅x	18	4	30	120
⚃⚃⚄⚄x	18	4	30	120
⚃⚃⚅⚅x	20	4	30	120
⚄⚄⚅⚅x	22	4	30	120

Hands with Two Degrees of Freedom

Run of Three

There are 4 runs of three: ⚀⚁⚂xy, ⚁⚂⚃xy, ⚂⚃⚄xy, ⚃⚄⚅xy. However, x cannot equal y (else we have run of three + doubles), x and y cannot both equal numbers in the run (else we have two doubles), and neither of x and y can equal a fourth part in the run (else we have a run of four).

For a run of three with no duplicates (for example, ⚀⚁⚂⚄⚅), there are 5!=120 permutations. For a run of three with one duplicate, there are 5!/2!=60 permutations.

Hand	Score	Count	Permutations	Odds
⚀⚁⚂xy;x∈{⚀⚁⚂},y∈{⚄⚅}	6	6	60	360
⚀⚁⚂xy;(x,y)=(⚄,⚅)	6	1	120	120
⚁⚂⚃xy;x∈{⚁⚂⚃},y=⚅	9	3	60	180
⚂⚃⚄xy;x∈{⚂⚃⚄},y=⚀	12	3	60	180
⚃⚄⚅xy;x∈{⚃⚄⚅},y∈{⚀⚁}	15	6	60	360
⚃⚄⚅xy;(x,y)=(⚀,⚁)	15	1	120	120

Triple

There are six possible triples, each with two degrees of freedom (x,y). x cannot equal y, neither of x and y can equal the tripled number, and x and y cannot form a run of three with the tripled number. There are then (52-5)/2-R=10-R ways to make each triple, where R is the number of runs of three containing the tripled number.

Hand	Score	Count	Permutations	Odds
⚀⚀⚀xy	3	9	20	180
⚁⚁⚁xy	6	8	20	160
⚂⚂⚂xy	9	7	20	140
⚃⚃⚃xy	12	7	20	140
⚄⚄⚄xy	15	8	20	160
⚅⚅⚅xy	18	9	20	180

Hands with Three Degrees of Freedom

Doubles

There are six possible doubles, each with three degrees of freedom (x,y,z). None of x, y, and z can equal each other, none of x, y, and z can equal the doubled number, and x, y, and z cannot form a run with the tripled number. There are then 5!/(3!*(5-3)!)-R1-R2 =10-R1-R2 ways to make each double, where R1 is the number of runs of three (4) and R2 is the number of runs of four containing the doubled number.

Hand	Score	Count	Permutations	Odds
⚀⚀xyz	2	5	60	300
⚁⚁xyz	4	4	60	240
⚂⚂xyz	6	3	60	180
⚃⚃xyz	8	3	60	180
⚄⚄xyz	10	4	60	240
⚅⚅xyz	12	5	60	300

Other Hands

Other hands are not possible with 5 dice, but I did not bother to prove this more formally. Instead, I can show that all hands are accounted for: there are 6^5=7776 possible rolls (in order), and the sum of all the “Odds” of the above hands is 7776. Results

Now we can sum the odds by score (instead of by hand) and normalize them. This gives us the following distribution.

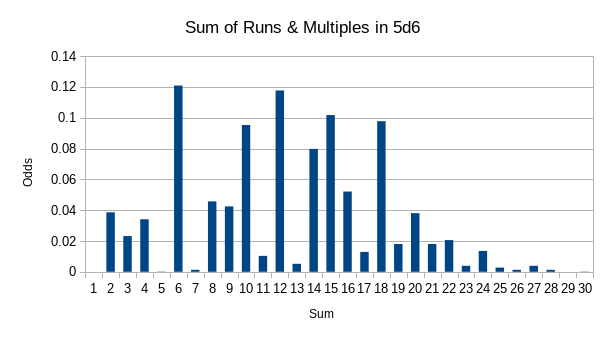
Score	Odds
1	0
2	300
3	180
4	265
5	1
6	940
7	10
8	355
9	330
10	741
11	80
12	915
13	40
14	620
15	791
16	405
17	100
18	760
19	140
20	296
21	140
22	160
23	30
24	105
25	21
26	10
27	30
28	10
29	0
30	1

The minimum score is 2, maximum 30, mean ~12.4, median 11, and mode 6. My spreadsheet is a bit messy, but you can see it here. Let me know if anything here seems off.

This post was first shared on February 17, 2020.

---

1. “Asked” is a strong word. Nobody asked for this.↩︎

2. In the case of ⚀⚀⚁⚁⚂, both run of three and two doubles would score 6. For convenience, we will consider it as two doubles, because restrictions to exclude it are already part of the math for a run of three.↩︎

---

---

---

---

---